Homemade Panera Bread Broccoli Soup is one of my favorite restaurant foods made at home!
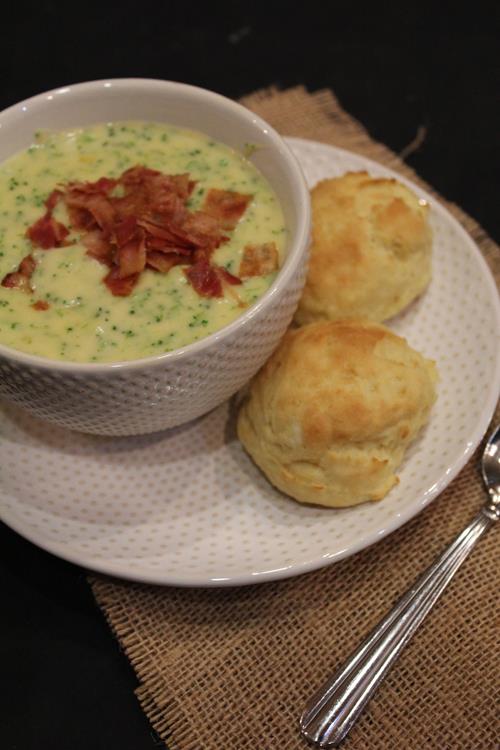
This recipe was one of the first that I posted on this site and it is still a favorite of my family. However, the post was poorly written, it contained only a few sentences. It was also hard to find on my site because it was titled “Dinner” and that was all. I really should have come up with a better title than that.
I have recently received several emails from readers asking me to repost this recipe so that they could easily find it, so I knew that I needed to update it.
Now only that, fall is coming soon and it will be the perfect time to make soup. So, I thought it would be a great time to repost my favorite soup.
I love Panera Bread soups. I especially like their broccoli soup, but I think they are expensive for what you get. I knew I could come up with something similar to make at home. I tried for quite awhile to make one close to it, but could not get it right. I tried several online recipes, but none tasted just right to me.
I took what I liked from several recipes and I came up with my own version. My family thinks my version is as good if not better than the one you get at Panera’s. I know it is much cheaper than taking my family out to eat.
This is a nice creamy soup and a great way to get your kids to eat broccoli.
For those of you that have been reading my site for awhile, have you tried this recipe?
Homemade Panera Bread Broccoli Cheddar Soup
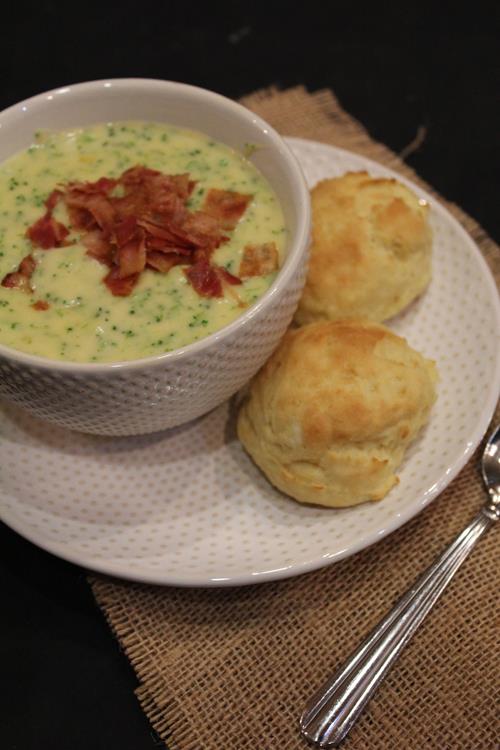
Homemade Paneray bread broccoli soup is a delicious make at home version of a favorite soup.
Ingredients
- 5 cups broccoli florets (if you have a little more or a little less that is fine)
- 6 cups chicken broth
- 1 1/2 cups milk or 1/2 & 1/2 (1/2 & 1/2 does taste better but I usually use milk)
- 1/2 cup plus 2 tablespoons flour ( Bob's Red Mill Gluten Free 1 to 1 Blend works well in this too)
- 2 cups grated cheddar cheese
- bacon, cooked and chopped (optional)
Instructions
- Steam broccoli until tender, about six minutes. Chop finely. I do mine in the food processor because we like it really chopped up and it is quicker. Set aside.
- In a large saucepan combine broth and milk. Slowly whisk in flour. Cook over med to med high heat stirring.
- Cook until it starts to thicken, but is not too thick. Usually just until it starts to boil.
- Add chopped broccoli. Reduce heat to med low. Continue to cook about 5 minutes.
- Add cheese stir until cheese melts.
- Serve.
- If using bacon sprinkle each bowl with a little.
Nutrition Information:
Yield:
8Serving Size:
1Amount Per Serving: Calories: 212Total Fat: 13gSaturated Fat: 7gTrans Fat: 0gUnsaturated Fat: 5gCholesterol: 40mgSodium: 1013mgCarbohydrates: 13gFiber: 3gSugar: 5gProtein: 13g
Nutritional values are approximate and aren't always accurate.

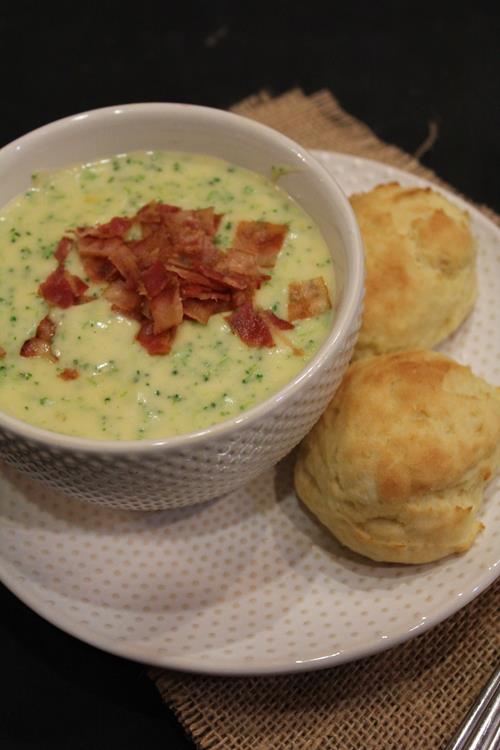

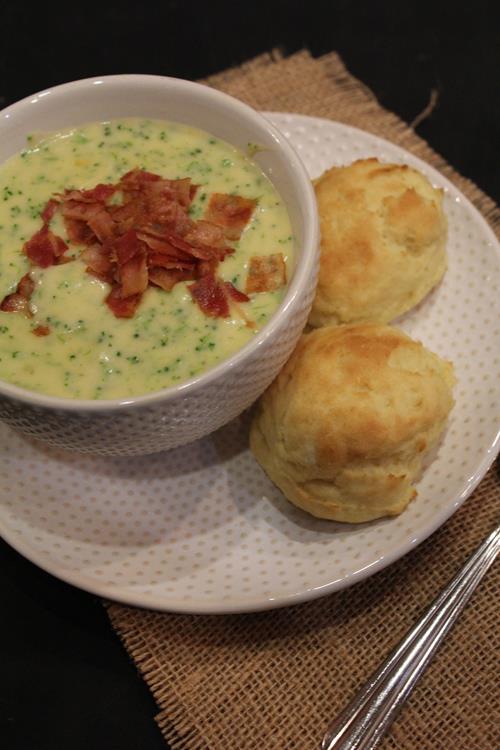

My recipe is very similar to this one and we love it!! Thanks.
I saw this last time you posted it. I’m so making it for Soup & Sandwich night.
Thanks for sharing!
~Liz
I love veggie soups and broccoli is one of my favorites. THANKS!!! for the recipe. Geri
I am a huge Panera fan and love making their dishes at home, also! I make a version similar to this soup, but I love the idea of adding the bacon – yummy! I also posted a Panera-like recipe today, for a Balsamic Vinaigrette that is similar to Panera’s Classic Cafe Salad.
thanks for the recipe daughter loves this soup
love that it doesn’t have onions (allergic)!
thanks again!
This was so good. We had it today for lunch, alongside some baked chicken – it made more than enough for several meals for our little family, and it was so simple, too. Thanks for sharing it! 🙂
I tried this a few weeks ago and loved it. I wanted to make it again today, but my broccoli was too far gone so I tried it with cauliflower. Yum!! Just as good. 🙂 Thanks for a great and easy recipe.
I am planning on making a double batch of this and then freezing half of it. I have never frozen soup before does this recipe freeze well?
@Chrissy, I have never frozen this. If you try it let me know how it turns out.
This sound really good. I’m adding it to my menu plan for next week.
.-= Allison´s last blog ..POM Wonderful Vinaigrette =-.
Sams Club sells the Panera Broccoli Cheese soup! I believe it’s $10 for a big container. I’ve tasted it and it is exactly like in the restaurant!
.-= Vicki´s last blog ..Trader Joe’s and Sprouts =-.
Oh my, I am sssooo excited to try this. My sweet husband never orders anything but this soup at Panera. If only I had time to make a fancy bread bowl, too. haha 🙂
I will definitely have to try your recipe. I tried another one from the internet and it wasn’t a good match. It called for pureeing it and the PB soup is definitely NOT pureed! However, yours is missing a key ingredient, IMO: the julienned (or shredded from the grocery store) carrots. It takes about 1 to 1-1/2 cups. I would just steam them with the broccoli or add them tot he broth/milk while cooking.
Thanks!
I make something really similar to this, and I throw some carrots into the puree-ing just for some more veggies. No one ever notices! Woo hoo!
This probably negates any sort of nutritional benefit from this soup, but it is to-DIE-for when you have crescent rolls (from the can!) on the side. Yummmm.
This looks delicious, thanks for sharing!
Any news on the freezing?? Would love to make this for my son who will no longer eat broccoli that is smooth, but we would not eat the whole pot before it would go bad. Thanks!
Cream soups do not freeze well, as they tend to separate. You can omit the cream and cheese, split the recipe to freeze, and then add them to the portion that you are using at the end. When you reheat the frozen portion you’ll have to add the cream and cheese then, as well.
Well, I didn’t try freezing it (yet) but I did make the soup and it was wonderful!!! And my son ate BROCCOLI again!!!!! Thanks.
@Jamie, I am so glad you liked it. And that is great that your son loved broccoli served this way. My family loves this soup.
This is FABULOUS. I’m eating it as I type. I actually used to work for Panera (though I worked in a corporate office, not in a bakery-cafe – I did eat their broccoli cheddar soup A LOT) and this is just as good (if not better!). I’m sure it’s much healthier too!
Thanks so much for this. I don’t think I need to go back for this again! 🙂
@Christan/MamaBearPing, That is quite the compliment!! Thank you so much and I am so glad that you enjoyed the soup. It is a favorite in our house.
Ohhh… delicious! And it’s 10 in the morning here- ha! This afternoon/evening are going to be CRAZY busy and my hope is that this will warm up okay for supper alongside my homemade baguette. If it tastes half as good as it does right now, we’re in luck! 🙂 (Happy Birthday!!)
@JessieLeigh, I am so glad that you enjoy it. Thanks for letting me know. I hope you have a Merry Christmas and that your daughter has a wonderful birthday!
Oh, Lynn … this is divine. I was in the mood for Broccoli Cheese soup this evening (impending snowstorm on the way!) and saw your post about Panera’s tomato soup, linking to this. Absolutely delicious. This will now be my go-to broccoli-cheddar soup. Thank you, thank you, thank you!
@Melissa, I am so glad that you enjoyed it! It is a favorite in our house and I am so happy that it is now one of yours.
Do you think his soup would be ok if all I have is frozen broccoli?
@Elaine, I think it would work fine, but it might change the texture a little since the frozen would have more moisture. But I think it would work okay.
I tried this recipe last night and it turned out great! I used frozen broccoli, and it tasted fine. My only wish that it was a little creamier. I will definitely make this again, but might try half and half instead of milk (all I had was 2% milk). Thanks for the recipe!
We tries this soup last night. Yum! I served this with toasted hot dog buns and red grapes. The kids ate it up! “ohh these are fancy breadsticks” lol
I had trouble with the flour. It clumped up 🙁 I used my fine mesh strainer to skim the clumps and mash back through. I think the soup would be thicker (for those of us not using 1/2 & 1/2) if the flour was whisked in with the milk.
Gave this a try tonight. I had to modify it with what we had, but the recipe was a great guide. It was a hit. Thanks.
MY first batch I made exactly the way the recipe called! Yummy yummy yummy! The next batch I added a little garam masala and it was even more divine! ( if that is possible!) for those who have asked, you can freeze this soup before the dairy products are incorporated into the soup. Wonderful recipe! So many leaping points for leftovers! Thank you for posting this gem!
So glad you liked it! And thanks for sharing your tips.
This was fantastic. I made it just as you said. I really was surprised that it didn’t require any other seasoning! Thanks for sharing. This is a keeper.
Lynne, I was wondering if you’ve tried this recipe with GF flour and if you have, what type of flour or flour mix would work with this recipe? Thanks so much!
Yes, I now use either cornstarch or potato starch and both work. The soup is a little silkier ( I guess that is the best way to describe it) than it was before, but it does work. I use about 1/3 of a cup and that amount seems to work okay. I need to measure it out exactly next time I make it so that I can share how exactly I do it gluten free.
I have some half & half I need to use up before February AND a ton of broccoli. Does this freeze well? I sure hope so… Sounds wonderful!
Ahh, just read that my freezing question has been answered. Looks like I’ll have to find another way to use up that half & half 🙂 This would still be a winner for lunch, though.
Made this for the first time tonight. It was a HUGE hit. I made home made bread bowls to go with it…..they LOVED it! Thank you for sharing so many wonderful recipes!!!
Just made this afternoon for lunch….it was really good and comes together in no time!! Thanks for a great soup recipe, I’ll be making it again!
So glad that you enjoyed it! Thanks for letting me know.
Hi, very neat site you have.. I do have a question.. chicken broth… how do you make that?
Made this tonight! Best broccoli soup I have ever had! Thanks so much!
Thanks! I am so glad that you enjoyed it.
We just had this for dinner and it was soooo good! I used a 12oz can fat free evaporated milk and it was so creamy. Thanks for another great recipe.
Hi Lynn,
How much time does it take to make this?
Thanks!
Csilla
I would say around 30 minutes if you included the prepping of ingredients, cooking, etc.
I can’t wait to make this soup. It is one my favorites but I have never found a recipe that looked like what I was looking for. Thanks so much. I’ll let you know how it comes out.
Jackie
I hope you enjoy it!
I made this today and was extremely disappointed in it – it is tasteless. I kept adding salt but it didn’t help. I checked the recipe on your website again and I did everything the recipe called for. I wasted my ingredients!!
Take this down.
Does this have that “flour-y” taste from using flour in the main part of the soup? Has anyone ever tried using arrowroot powder and if so, what were your results? The reason I ask is because I know when I made gravy as a young cook (eons ago!) it always tasted flour-y, so I learned to brown the flour first. It made all the difference in the taste of my gravies. About 10 or 12 years ago I started using arrowroot (it takes less so be careful if you try it) and that eliminated the flouriness flavor. Over the years I’ve grown to depend on arrowroot (Bob’s red mill is a good one but there are lots of others now, in health food stores and food co-ops) for thickening lots of things like homemade pie fillings, puddings, etc.
I don’t think it has a strong flour taste, but I don’t mind that in most recipes. I have not done a lot of cooking with arrowroot, but if you have used it in other similar recipes than I think it should work fine in this one. I would just substitute it like you have in other recipes. The flour is just helping to thicken the soup. I have used potato flour in this recipe for an easy gluten free version and it worked fine. So I think you could use other thickeners in it. I hope that helps.
Oh, I have some potato flour on hand, too, I could try that. Thanks for the suggestion!
If the half n’ half tastes better, why do you use milk in your personal recipe?? CREAM IS GOOD FOR YOUR BODY. All of this business about “high cholesterol ” has been proved to be pure medical propaganda. Eat real butter from a good source (grass fed is best) use real cream, use full-fat milk (not the 2% or 1% crap being passed off as milk when in reality it’s nothing but water with chalk in it.
If you’re looking for good advice on staying healthy against the commonly spewed nonsense, read at Dr. Malcolm Kendrick’s site. He tells it like it is. I’ve read all of his books, but the best was Doctoring Data. That’s what happens – – between the medical industry and the food industry, they doctor the data to scare the pants off of people. Are they really going to try to tell me that what’s taught nowadays, foodwise, when the average life span is 65-70, is actually better than what my grandparents all ate (REAL FOODS unadulterated) and all lived well into their 90’s, one was almost 100?? Nah, I don’t think so.
But this recipe sounds like something I’d like and I’m going to give it a try tomorrow after going to the health food store for the broccoli and cream. Thanks for posting it. I was actually just thinking about soups because the weather here has been COLD!